Entropy computation
Entropy computation can be expensive. In particular in malware analysis, many heuristics need to compute the entropy of a lot of different regions of the file: a section, a long string, etc. Complexity can quickly add up. That’s why Malcat takes a somewhat different approach than the usual Shannon entropy in order to get better performances.
Entropy approximation
Shannon’s entropy computation requires several log2 computations and divisions which are all expensive operations. But most of the time for malware analysis, users are not really interested in the Shannon entropy value of a data block. They just want to know if the block is packed / compressed or not. This can be approximated using less expensive operations.
Malcat approximates entropy using a sliding window algorithm which roughly computes the number of unique bytes in each window. To compute the entropy of a file interval, Malcat will go over the file interval using a window of 64 bytes. For every 64 bytes block, the number of unique bytes is computed (so a number between 1 and 64). Intuitively, a window containing packed / crypted data will have a number of unique bytes near 64. Low-entropy data will have many similar bytes, thus a low number of unique bytes.
Then, the mean between each window’s unique bytes count is computed and adapted to get a value between 0 and 255. This is Malcat’s entropy.
Entropy cache
Having a fast entropy approximation is good, but entropy is often needed at a lot of different places and is thus called alot. For instance, the entropy of each section and each string is computed in malcat. It is also used in many different anomalies. Having to compute entropy again and again on the same data can quickly become expensive. That’s why Malcat use an entropy cache.
When Malcat computes the entropy of a file, it divides the file into N blocks, where N is 512 by default, but can be changed in options: . Then Malcat stores the entropy of each of these 512 blocks in cache. Querying entropy over a file range in malcat is going over this list of cached block entropy values and taking the mean of them. It means that:
Querying entropy of a file range of size N in Malcat has a complexity of O(G) where G = number of blocks
Entropy of small intervals is very imprecise in Malcat. Given a 1Mb file for instance, entropy blocks are 2KB big. It means that if you query entropy for a 10 bytes buffer, you will get the entropy of the surronding 2KB buffer instead, which can be greatly different. On the other hand, computing entropy of small blocks has very little meaning anyway.
We re well aware that Malcat’s approach is far from perfect. We’ve chosen to give priority to performances, and it has its downsides.
Entropy usage
Since it is so cheap, Malcat’s cached entropy is used in many different places. It is used in the Augmented navigation bar of the Hexadecimal view and the Structure/text view. It is also used in File layout screen of the Summary view.
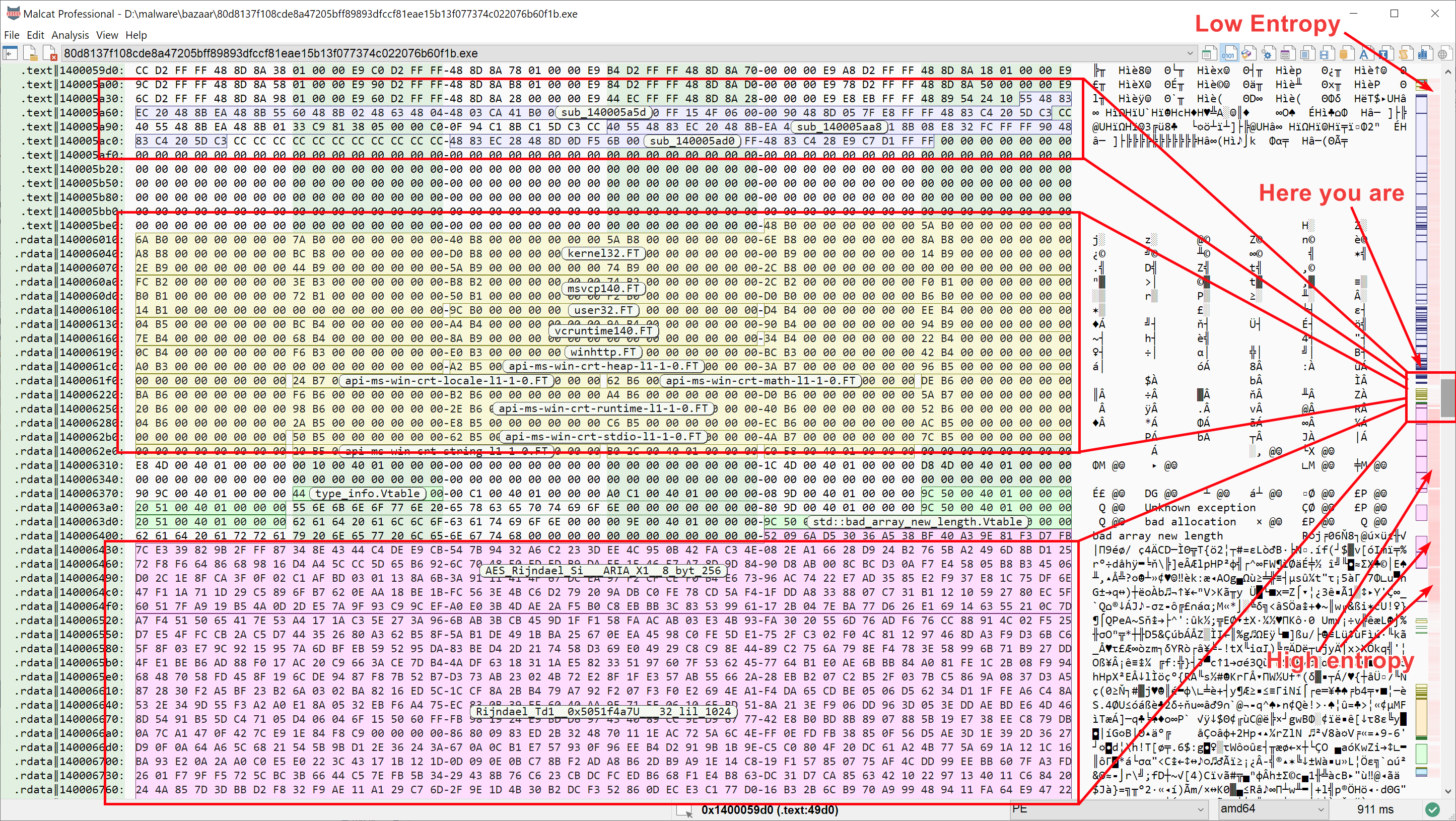
Entropy in the hexadecimal view’s augmented scroll bar
Entropy is also used in String analysis (each string has an entropy score), and several Anomaly scanner also makes use of entropy (e.g. BigBufferNoXrefMediumToHighEntropy).